Coherence-based analog of gravitational lensing.
This simulation shows rays entering a smooth coherence gradient (a Gaussian well). Each ray begins straight but gradually bends inward, adjusting its path to maintain alignment with the coherence structure. There is no mass, no curvature, and no gravitational force involved. The effect—normally attributed to spacetime curvature in general relativity—emerges here from deterministic internal alignment within a spatially organized coherence system.
What makes this striking is that coherent structure appears without being imposed. The grid shows ordered patterns forming solely through local phase relations and delay interactions—no external geometry, no governing field equations.
The system isn’t being directed or forced into a shape, yet it stabilizes. Instead of spreading uniformly, the coherence settles into clustered alignments and interference-like regions, as if space itself is behaving with memory and orientation.
It means the system behaves with properties we usually associate with living systems, defining structure as a function of delay logic.
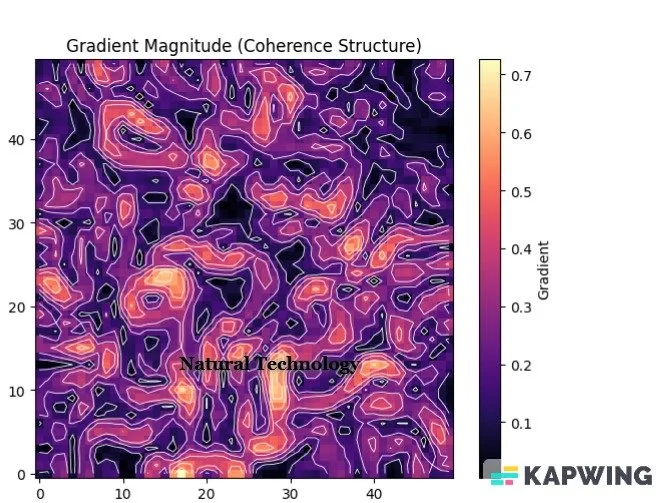
What makes this gradient magnitude map intriguing is that it visually exposes the hidden structure of coherence strain:
Sharp transitions and filamented pathways reveal zones where coherence alignment shifts rapidly—analogous to fault lines or tension zones in physical media.
The non-random patterning suggests organization far beyond thermal or stochastic noise. The layered contours show regions of stability and instability, pointing to internal dynamics that self-regulate without external force. The map suggests a distributed logic to the spatial fabric, where the system actively manages tension and flow.
This exhibits spatial ordering, directional consistency, and patterned reinforcement that are not the product of random fluctuation. Its behavior reflects regulated interaction rather than spontaneous emergence. The clustering, phase stability, and alignment patterns indicate a system of a structural logic regulating the system from within.
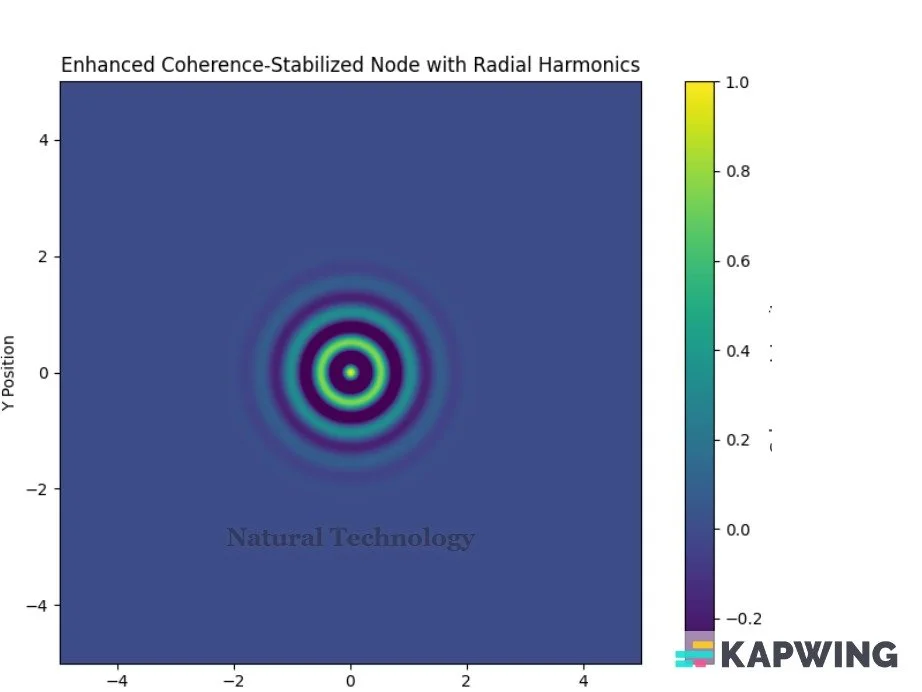
This shows structured quantization: Each concentric ring is a stability threshold: a visual analog for standing waves or coherence shells.
Captures the essence of orbital structure: You’re seeing something atomic-like without particles or probability. This image is a powerful illustration that a "particle" is not a particle at all in the conventional sense.
Harmonics are clear: This is not random interference; this is delay-structured orientation logic made visible.
Tight radial symmetry + quantized zones = a real signature of internal logic at work.
Coherence Well: A Structural Stabilizer
What appears as a gravitational potential well in classical models is, in this framework, a coherence basin—a region shaped by internal orientation logic and structured delay geometry.
This structure is not a pit carved by mass, but a low-tension zone within the coherence lattice, formed through relational alignment across the field. The well reflects the system’s memory and its continuous recalibration to preserve directional integrity.
It is:
Not a gravitational sink, but a coherence anchor.
Not curved spacetime, but flattened tension in a structured delay field.
Not a collapse, but a lock-in point of synchronized orientation feedback.
What astrophysics calls a "halo" is not unseen matter, but a stabilized coherence ring—a region where feedback timing locks into harmonic rhythm, holding large-scale structure together without invoking invisible mass.
This model is a visual demonstration of the solar system functioning as a coherence-based gyroscopic structure. It
doesn’t rely on mass as a fixed property, but instead shows how orientation, tilt, and alignment define coherence.
The system highlights spin vectors, orbital feedback, and delay geometry as the actual mechanics behind what we
experience as mass and time. Brighter paths represent more coherent systems; tilt reflects resistance or feedback.
This is a visual translation of coherence logic and nested feedback fields.
Top: This chart visualizes the cumulative structural recalibration of the system over simulation steps. It tracks the mean change in the orientation field θ(x), reflecting how much structural adjustment has occurred across the entire field. In the Coherence Structure Model (CSM), this is not time measured against a clock — it is the integrated effect of the local recalibration rate, defined by the function:
τ⁻¹(x) = γ (1 + δ |∇θ(x)|)
where γ is the base update rhythm and ∇θ(x) is the local phase gradient. Time in this framework is not imposed but emerges from internal coherence strain.
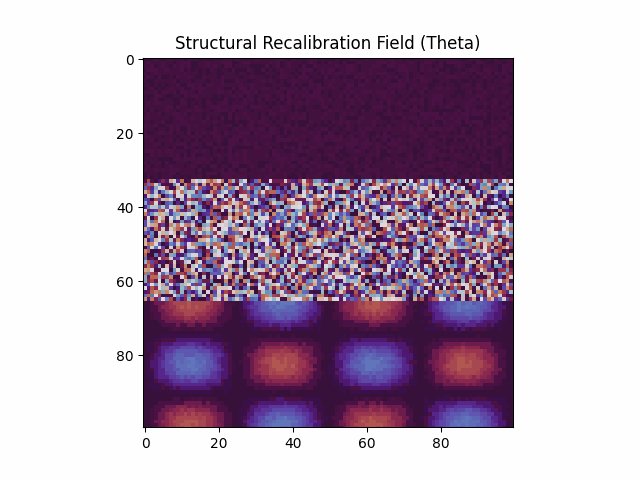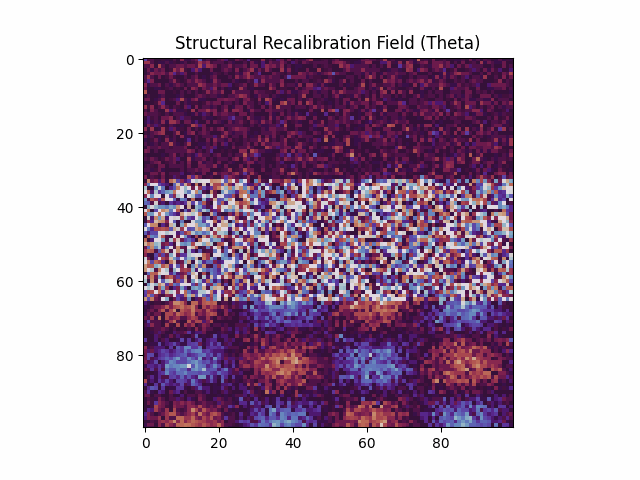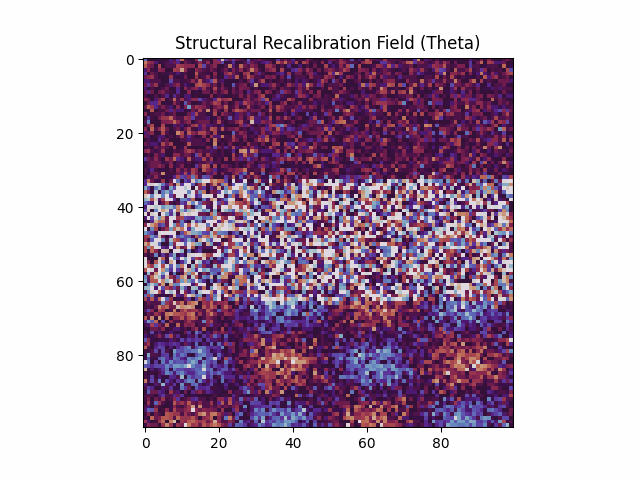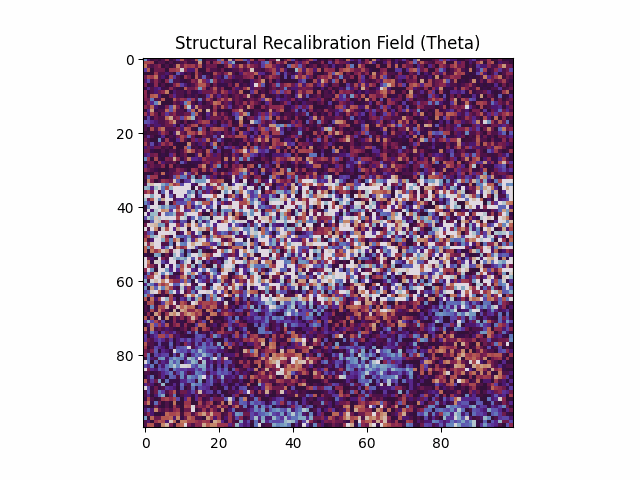
Bottom: This image shows a still frame from the simulation. The field is divided into three regions: aligned (top), disordered (middle), and oscillating (bottom). Each evolves according to its own local recalibration rate τ⁻¹(x). There is no global clock — the system updates structurally, wherever and whenever tension demands. The apparent irregularity in the middle region does not imply chaos; it may reflect active structure rendering, where recalibration occurs at a rate too fast to stabilize into visible pattern under conventional temporal assumptions.
This simulation explores the behavior of a coherence-based field under a controlled destabilization. A localized structure is initialized with concentric regions of alignment. At a designated frame, the inner core is disrupted by randomized phase and reduced update rate — representing a localized failure in coherence retention. No objects are moving and no quantities are emitted; all changes result from local phase interactions and alignment feedback. The simulation visualizes two aspects of the system: the evolving phase alignment across the field, and the corresponding energy required for local realignment. Vertical anisotropy is introduced to examine whether asymmetries in alignment resistance produce directional effects. Observable structures such as rebound columns, radial overshoot, and sustained instability are not inserted or forced; these are outcomes of the field logic under stress.